数学建模初尝
三林中学陆晓娥 浦东外国语顾晓琛 群星职校张艳
现在的中学课程改革加强了综合性、应用性的教学内容,重视联系学生生活实际和社会实践。这是在课程、教学中注入素质教育内容的具体要求。
近几年来,数学应用题的数量和分值也逐步被引进学科教学中,在交大,数学建模已成为学生的一个热门课,交大4支学生队伍在美国国际SARS数模赛中的599支队中遥遥领先,获4个一等奖。
但对我们来说数学建模却是一个陌生的课题,这个暑假,通过参加殷伯明老师的数模培训班,使我对数模这个课题产生了极大的兴趣,受益匪浅。
数学模型是为了一定目的,对客观事物的一部分进行简化、抽象、提炼出来的原型替代品。模型集中反映了原型中人们需要部分的特征。
数学建模,是用数学方法来解决真实问题的一种手段与技巧。数学建模与其说是一门技术,不如说是一门艺术。
数学建模的方法基本有:
1.机理建模:是根据对物机理的认识,找出反映事物变化的数量规律;机理建模适用于结构明确,数据完整,机理清楚的系统
2.数据建模:是通过对量测数据的分析,找出与数据拟合最好的模型;数据建模适用于结构不明确,数据缺乏,机理模糊的系统
3.二者结合:机理分析建立模型结构,数据分析确定模型参数,这种是比较常用,精确度相对较高的一种建模方式。
建模的步骤一般分:
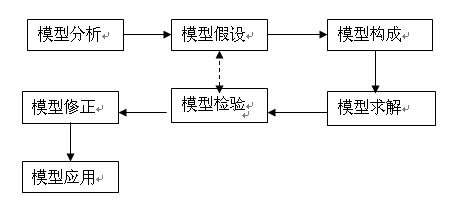
1.模型分析:了解问题的实际背景,明确其实际意义,掌握对象的各种信息。
2.模型假设:根据实际对象的特征和建模的目的,对问题进行必要的简化,并用精确的语言提出一些恰当的假设。
3.模型构成:在假设的基础上,利用适当的数学工具来刻划各变量之间的数学关系,建立相应的数学结构。(尽量用简单的数学工具)
4.模型求解:利用获取的数据资料,对模型的所有参数做出计算(估计)。
5.模型检验:将模型分析结果与实际情形进行比较,以此来验证模型的准确性、合理性和适用性。如果模型与实际较吻合,则要对计算结果给出其实际含义,并进行解释。如果模型与实际吻合较差,则应该修改假设,在次重复建模过程。
6.模型修正:根据检验结果,与历史数据相比较,对模型进一步修正。
7.模型应用:应用方式因问题的性质和建模的目的而异。
通过这次短短4天的培训,使我对数学建模的意义有了一定的理解,体会到了数学的应用价值,培养了我对数学的应用意识;增强了数学的学习兴趣,学会团结合作,提高分析和解决问题的能力;同时也培养了我利用数学进行计算机学科教学的创新能力。
2009-05-16
